Fungsi Komposisi

Fungsi komposisi merupakan penggabungan operasi dua jenis fungsi f(x) dan g(x) sehingga menghasilkan sebuah fungsi baru. Operasi fungsi komposisi biasa dilambangkan dengan "o" dan dibaca komposisi atau bundaran. Fungsi baru yang dapat terbentuk dari f(x) dan g(x) adalah:

1. (f o g)(x) artinya g dimasukkan ke f

2. (g o f)(x) artinya f dimasukkan ke g

Fungsi tunggal tersebut merupakan fungsi yang dapat dilambangkan dengan huruf “f o g” atau juga dapat dibaca “fungsi f bundaran g”. Fungsi “f o g” adalah  fungsi g yang dikerjakan terlebih dahulu kemudian dilanjutkan dengan f. Sedangkan, untuk fungsi “g o f” dibaca fungsi g bundaran f. Jadi, “g o f” adalah fungsi dengan f dikerjakan terlebih dahulu daripada g.

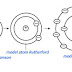
Untuk memahami fungsi ini, perhatikan gambar berikut:

Dari rumus di atas, definisi yang kita dapatkan adalah :

Jika f : A → B ditentukan dengan rumus y = f(x)

Jika g : B → C ditentukan dengan rumus y = g(x)

Maka, didapatkan hasil fungsi g dan f: h(x) = (gof)(x) = g( f(x))

Dari penjelasan di atas dapat disimpulkan bahwa fungsi yang melibatkan fungsi f dan g dapat ditulis :

• (g o f)(x) = g(f(x))
• (f o g)(x) = f(g(x))

Terdapat sifat-sifat pada fungsi komposisi yang dijelaskan pada gambar di bawah ini.

Jika f : A → B , g : B → C , h : C → D, maka berlaku :

Okay Squad, sekarang kita coba kerjakan contoh soal di bawah ini supaya kamu semakin mengerti dengan fungsi komposisi.

1. Jika f(x) = 2x + 3 dan (f o g) = 2x² + 6x – 7, maka berapakah hasil dari g(x) ?

Jawab:

(f o g)(x) = 2x² + 6x – 7

f(g(x)) = 2x² + 6x – 7

2 (g(x)) + 3 = 2x² + 6x – 7

2 (g(x)) = 2x² + 6x -10

Jadi, g(x) = x² + 3x - 5

2.  Jika (f o g)(x) = x² + 3x + 4 dan g(x) = 4x – 5. Berapakah nilai dari f(3)?

Jawab:

(f o g)(x) = x² + 3x + 4

f (g(x)) = x² + 3x + 4

g(x) = 3 maka,

4x – 5 = 3

4x = 8

x = 2

Karena f (g(x)) = x² + 3x + 4 dan untuk g(x) = 3 didapat x = 2

Sehingga : f (3) = 2² + 3 . 2 + 4 = 4 + 6 + 4 = 14